What is multiple linear regression?
Multiple linear regression (MLR), often known as multiple regression, is a practical solution that predicts the result of a response variable using numerous explanatory factors. Multiple linear regression attempts to represent the linear correlation between explanatory (independent) and response (dependent) variables. Multiple regression is essentially a supplement of ordinary least-squares (OLS) regression in that it incorporates more than one explanatory variable.
Comprehending Multiple Linear Regression
Simple linear regression allows statisticians to forecast the value of one variable based on knowledge about another. Linear regression aims to construct a straight-line relationship between two variables. A variant of regression in which the dependent variable has a linear connection with two or more independent variables is known as multiple regression. Non-linearity occurs when the dependent and independent variables do not follow a straight line.
Both linear and non-linear regression use graphs to monitor a specific response using two or more variables. Non-linear regression, on the other hand, is typically difficult to implement since it is based on assumptions acquired by trial and error.
Formula for MLR
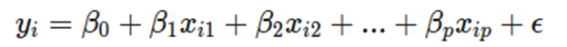
Where, for i = n observations;
yi = dependent variable
xi = explanatory variables
β0 = y-intercept (constant term)
βp = slope coefficients for each explanatory variable
ϵ = the model's error term (also known as the residuals)
Multiple linear regression computes three things to obtain the best-fit line for each independent variable:
· The regression coefficients with the lowest total model error.
· The entire model's t statistic.
· The corresponding p-value (the probability that the t statistic happened by chance if the null hypothesis of no link between the independent and dependent variables was valid).
The t-statistic and p-value are then computed for each regression coefficient in the model.
Relevance of MLR
Simple linear regression is integral that enables a financial or statistical analyst to estimate one variable based on knowledge about another one. Linear regression can only be employed when two continuous variables exist, independent and dependent. The parameter that is utilized to compute the dependent variable or result is known as the independent variable. A multiple regression model includes many explanatory variables.
The coefficient of determination (R-squared) is a statistical metric to determine how much variation in the result can be explained by changes in the independent variables. R2 constantly rises when additional predictors are added to the MLR model, irrespective of whether the predictors are unrelated to the outcome variable.
R2 cannot thus be used to determine which predictors should be part of a model and which should be discarded. R2 is limited to 0 and 1, with 0 indicating that none of the independent variables can predict the outcome and 1 indicating that all independent variables can predict the result without mistake.
When analyzing multiple regression findings, beta coefficients are actual when all other variables are held constant ("all else equal"). Multiple regression results can be shown horizontally as an equation or vertically as a table.
Multiple Linear Regression Assumptions
The following assumptions underpin multiple linear regression:
i. A connection between the dependent and independent variables that is linear.
The basic assumption of MLR is that the dependent variable and each of the independent variables have a linear relationship. Creating scatterplots and visually inspecting the scatterplots for linearity is the best technique to validate the linear connections. If the scatterplot shows a non-linear relationship, the expert must conduct a non-linear regression or modify the information provided using statistical software like SPSS.
ii. There is no strong correlation between the independent variables.
Multi-collinearity, which arises when the independent variables (explanatory variables) are highly interrelated, should not be present in the data. When independent variables exhibit multi-collinearity, it is difficult to determine which variable contributes to the variance in the dependent variable. The Variance Inflation Factor approach is the most effective for testing the assumption.
iii. Observational independence
The model implies that the observations are unrelated to one another. As expressed, the model suggests that residual values are independent. The Durbin-Watson statistic is used to test this assumption.
The test returns results ranging from 0 to 4, with values ranging from 0 to 2 indicating positive autocorrelation and values ranging from 2 to 4 indicating negative autocorrelation. The midpoint, a value of 2, means no autocorrelation.
iv. Normality in several variables
When residuals are regularly distributed, multivariate normality arises. Examine the distribution of residual values to put this assumption to the test. It may also be examined using one of two methods: a histogram with an overlaid standard curve or the Normal Probability Plot.
v. Residual homoscedasticity
Homoscedasticity, or variance homogeneity, is the concept that variations in various groups are equal or comparable. Since parametric statistical tests are conscious of differences, this is a crucial assumption. Inconsistent sample variance leads to misleading and distorted test findings.
vi. Notable outliers, high-leverage spots, or points of strong influence
There should be no notable outliers, high-leverage spots, or points of strong influence. Outliers, leverage, and influential points are all phrases used to describe observations in your information set that are out of the ordinary while performing a multiple regression analysis. These many classes of odd points reflect their various effects on the regression line. An observation might include many types of unexpected points and unrelated variables.
Applications of MLR
For example, a financial analyst may be interested in seeing how market activity influences the costs of a given corporation, say, ExxonMobil (XOM). In this scenario, the S& P 500 index value will be the independent variable or predictor, and the cost of XOM will be the dependent variable.
In actuality, several elements influence an event's result. ExxonMobil's stock price, for example, is affected by factors other than market performance. Other variables, like interest rates, the cost of oil, and the shift of oil futures prices, can impact the price of XOM and the stock prices of other oil firms. Multiple linear regression is essential in understanding a correlation between more than two variables.
Multiple linear regression (MLR) is a statistical method for determining a mathematical connection between numerous random parameters. In other words, MLR investigates how several independent factors relate to a single dependent variable. Establishing each independent variable to estimate the dependent variable implies that the data on the various variables may be utilized to forecast their influence on the result variable accurately. The algorithm generates a straight-line (linear) relationship that best corresponds to all individual data elements.
The multiple regression model enables an analyst to forecast an outcome based on data from numerous explanatory factors. However, the model is not always correct since each data point might diverge somewhat from the model's expected conclusion. To account for such minor fluctuations, the model includes the residual value, E, which is the difference between the actual and projected outcomes.
Limitations of multiple linear regression
Multiple linear regression is a popular tool in empirical policy research. The core thesis of this work is that most of this use is incorrect, not due to the multiple linear regression approach but due to the nature of the data employed. Too often, analysts are led beyond justifiable conclusions into claims for which there is virtually no solid response, resulting in questionable policy recommendations. Four policy interpretations are proposed: causal models, simple prediction, primary data set descriptions, and causal predictive models. Policy analysis favors assertions of the latter kind, whereas multiple linear regression analysis of passively observed data favors claims of the former. The study investigates the inferential logic and technical challenges that develop as the student progresses through the four classes. The research then explores the function that multiple linear regression of passively observed data might play in policy analysis and recommends alternate techniques.
What is the distinction between linear and multiple regression?
Ordinary linear squares (OLS) regression examines a dependent variable's response to changes in some explanatory factors. On the contrary, a single variable seldom describes a dependent variable. An analyst employs multiple regression in this scenario to explain a dependent variable using more than one independent variable. Multiple regressions can be linear or non-linear.
Multiple regressions are predicated on the premise that the dependent and independent variables have a linear relationship. It also presupposes that there is no significant association between the independent variables.
How to compute linear regression model error?
Linear regression frequently uses mean-square error (MSE) to calculate the model error. MSE is computed as follows:
· Computing the mean of each of the squared distances; measuring the distance of the observed y-values from the anticipated y-values at each value of x.
Linear regression finds the regression coefficient with the least MSE and fits a line to the data.
What characterizes a multiple regression?
Multiple regression analyses the impact of more than one explanatory variable on a given result. It assesses the relative effect of these explanatory or independent factors on the dependent variable while maintaining all other variables constant in the model.
Why would a multiple regression be preferable to a simple OLS regression?
A single variable rarely explains a dependent variable. In such instances, an analyst does multiple regression, which seeks to define a dependent variable by utilizing more than one independent variable. The model, on the other hand, assumes that there are no significant correlations between the independent variables.
Can I perform a multiple regression on my own?
Multiple regression models are complicated, and they get much more so when more variables are added to the model or the amount of data to evaluate expands. Multiple regression analysis will need specialized statistical tools or functionality inside applications such as Excel.
What does "linear" imply in multiple regression?
The model in MLR computes the line of best fit that optimizes the variations of each of the variables incorporated as they relate to the dependent variable. It is a linear model since it fits a line. Non-linear regression models with many variables, such as quadratic regression, logistic regression, and probit models, are also available.
How do multiple regression models apply in finance?
A multiple is any econometric model that considers more than one variable. Factor models examine the links between variables and the consequent performance by comparing two or more factors. The Fama and French Three-Factor Mod is a model that extends the capital asset pricing model (CAPM) by including size and value risk components in addition to the market risk factor in CAPM (which is a regression model). The model accounts for this outperforming tendency by integrating these two additional criteria, making it a more robust tool for measuring management effectiveness.
The distinction between multiple linear regression and logistic regression
Multiple linear regression can reveal one or more probable associations between elements, like in repercussions relationships; however, in logistic regression, independent factors have no associations because they are entirely independent and have no dependent factors.
Conclusion
Multiple linear regression is an empirical method for predicting the result of a variable using the values of two or more variables. It is a variant of linear regression and can be referred to simply as multiple regression. The parameter that is supposed to be estimated is the dependent variable, and the elements we use to forecast the outcome of the dependent variable are explanatory or independent variables. The approach allows statisticians to calculate the model's variability and the corresponding part of each independent variable to the overall variance.
