What is Net Present Value?
The future profitability of an investment, project, or enterprise may be estimated using its net present value. The net present value (NPV) of an investment is the discounted total of all cash flows expected during the investment's lifespan.
Net present value is a common tool used in budgeting for determining where and when money should be spent. Financial experts are better able to make calculated judgments when all investment possibilities and possible projects are reduced to the same level; how much they will be worth in the end. The Net Present Value (NPV) of an investment must first be valued using the Discounted Cash Flow (DCF) method. In the end, a discounted cash flow analysis will provide an NPV.
Who Makes Use of NPV?
In corporate finance, NPV is the primary metric of choice. When deciding whether a merger or acquisition is the best investment, investment bankers may use net present values to make a decision. In addition, qualified management accountants and other accountants may use NPV to manage finances and set project priorities. The ability to compute a net present value (NPV) is useful for company owners in many ways, including budgeting and forecasting.
The formula for the Net Present Value (NPV)
NPV is determined by calculating the costs (negative cash flows) and benefits (positive cash flows) for each period of an investment. To get the net present value of an investment or project, one must first determine its expected cash flows throughout its expected time period, discount those cash flows to the present, and then deduct the original investment from the total discounted cash flows.
The formula is as follows:
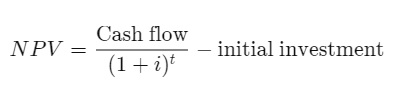
Where:
i = Required return or discount rate
t = number of time periods
To determine a project's NPV based on multiple cash flows received over a long period of time, then the formula is as depicted below:
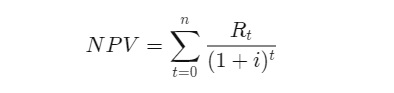
Where:
Rt = net cash inflow-outflows during a single period
ti = discount rate or return that could be earned in alternative investments
t = number of time periods
Here's a simpler method to recall the idea of NPV if you're not familiar with summation notation:
NPV = Today's value of the expected cash flows - Today's value of invested cash
NPV may also be analyzed by the use of spreadsheets (for example, Excel), financial calculators or tables.
Elements of NPV
- Number of periods (n)
In other words, the duration of the project or investment is represented by the number of periods. Since 10 years is about the typical lifetime of a corporation, it is sometimes the default value for the number of periods. However, certain timelines may be associated with a variety of initiatives, businesses, and investments.
- Original investment
The upfront investment is the whole amount spent right away. If the overall discounted cash flows are to be calculated, for example, the initial project cost of $5 million must be deducted.
- Cash flow
Investment-related cash flows include items like capital expenditures, interest, and loan repayments. The cash flow statement for a certain time period accounts for all cash withdrawals and inflows.
- Rate of discount (r)
The discount rate is typically the weighted average cost of capital (WACC) of the firm. The WACC is the rate at which a firm must generate earnings in order to cover its operational expenses, which might include items like interest, loan payments, and dividends.
The temporal worth of money necessitates discounting cash flows. It's the idea that being paid presently is better than getting paid later. If you invest the money you get Today and earn interest over the next year, the value of your investment will increase, making $10 now worth more than $10 next year. Future cash flows are discounted to their present value so that we may more correctly assess investment possibilities in light of the impact of interest rates and inflation on the purchasing power of a dollar.
The information provided by Net Present Value
NPV takes into account the passage of time and may be used to evaluate the relative profitability of several projects or to determine if a proposed rate of return meets the minimum threshold necessary to proceed with an investment.
The discount rate in the NPV calculation represents the time value of money and might serve as a project hurdle rate depending on a company's cost of capital. A negative net present value (NPV) indicates that the predicted rate of return will be lower than the discount rate, which means that the project will not generate value.
Discounted cash flow (DCF) analysis is another name for the net present value calculation used in the context of assessing corporate securities. It's Warren Buffett's preferred approach for evaluating whether or not the present price of a firm is justified by the NPV of its future DCFs.
The discount rate plays a crucial role in the calculation. As long as interest rates remain positive, it takes into account the fact that one dollar now is worth more than one dollar tomorrow. Money loses purchasing power due to inflation. In the meanwhile, one may put Today's dollar into a relatively risk-free investment vehicle, such as a government bond; investments with a greater degree of uncertainty should provide a higher return. The discount rate, whatever it is calculated, is the minimum rate of return an investment must achieve in order to be profitable.
NPV Interpretation
There are three possible results for net present value:
- If the net present value (NPV) of a project or investment comes up positive, it may be worthwhile to go through with the endeavor.
- If the net present value (NPV) of a project or investment comes up negative, it's usually not a good idea to go on with it.
- If a project's or investment's net present value (NPV) is zero, it is neither financially beneficial nor prohibitive. Projects and investments with little NPV may still be considered if they provide substantial intangible advantages for the organization, such as improved strategic posture, brand equity, or customer pleasure.
Challenges of NPV
The analysis relies on assumptions about the future that may or may not come true, which is a significant drawback of NPV. As with the investment cost and expected return, the discount rate value employed is a matter of discretion. The validity of an NPV analysis depends on the accuracy of its assumptions.
Though easy to comprehend, the monetary result from the NPV formula is not always indicative of the whole picture.
Advantages and disadvantages of the NPV formula
Advantages
- The value of money over time is included in the NPV formula. The discounted net cash flows of an investment are taken into account in the NPV calculation to assess its viability.
- Businesses can make decisions using the NPV technique. It aids in not only comparing projects of the same size but also in determining whether a given investment is profitable or not.
- The cost of capital is used to discount future cash flows.
- NPV provides a single numeric number that is simple to understand.
- The numbers could be simple to put into a spreadsheet or a bank's calculator.
Disadvantages
- The basis for computing NPV is to use the needed rate of return to discount future cash flows to their present value. There aren't any rules for calculating this rate, though. Companies are free to choose this percentage figure, and there may be cases where the NPV was incorrect due to an incorrect rate of return.
- It is not applicable for evaluating projects of varying sizes. Net present value is a fixed number, not a percentage. As a result, it stands to reason that the NPV of bigger projects will be greater than that of smaller ones. It's possible that the NPV for the larger project is greater since the returns are higher than the investment.
- NPV significantly depends on assumptions, forecasts, and inputs.
- The formula ignores factors such as project size and ROI.
- Manually estimating this value might be challenging for projects with a long cash flow life.
Net present value vs Payback period
A significant factor for anybody with limited resources is the return on investment (ROI), which the NPV calculation does not measure. While the NPV formula may give you a good idea of how much value a project can generate, it cannot tell you whether or not your investment money will be well spent.
When compared to NPV, the payback time (or payback technique) is a more straightforward calculation. How long it will take to get your money back is what the payback technique is all about. This approach has the potential downside of disregarding the time worth of money. This is why there is more room for error in payback times computed for longer-term investments.
Furthermore, the payback time does not include what occurs after the initial investment expenditures are recouped. The rate of return on investment may fluctuate widely over time. Payback periods are used in comparisons assuming this is not the case.
Comparing Net present value (NPV) with Internal rate of return (IRR)
By computing the NPV formula for the discount rate that would bring the NPV to zero, the internal rate of return (IRR) may be determined. With this technique, you may evaluate the relative profitability of initiatives with varying time frames.
Can you explain the variance between NPV and IRR?
For every given investment, the discount rate that results in a negative net present value (NPV) is equal to that investment's internal rate of return (IRR). You might also see this from the perspective that NPV and IRR are attempting to address different but interconnected concerns. To calculate net present value, one must ask, "How much money will I make in total if I go through with this investment, factoring in the time value of money?" To calculate IRR, you must ask, "What is the yearly rate of return that I can expect if I make this investment?"
When should you use NPV?
A positive net present value (NPV) is considered "good" in principle. Because the discount rate used in calculating net present value already accounts for the investor's cost of capital, opportunity cost, and risk aversion, there is no need to worry about these elements in any further analysis. The time value of money and the project's expected future cash flows are also considered. Therefore, in theory, even an NPV of $1 would be considered "good," suggesting that the project is worthy. Since the projections used in the computation might be off, many planners will instead establish a higher criterion for NPV as a safety net.
Why do we put a discount rate on future cash flows?
The time value of money is reflected in NPV via the use of discounted cash flows. Since Today's dollar may earn tomorrow's worth of interest, it is worth more than tomorrow's dollar as long as interest rates remain positive. Even if it is possible to predict future returns with precision, such rewards will not be realized for quite some time, during which an equivalent amount of money might earn interest.
Conclusion
The monetary concept of net present value (NPV) aims to measure the whole worth of an investment opportunity. To compute NPV, first estimate all financial outputs and inflows associated with an investment, then discount those cash flows to the present and then add them all up. The NPV of an investment is computed by adding up all of its cash flows, both positive and negative. If an investment's net present value (NPV) is positive, it is a smart idea to proceed with it.
