What is a t-test?
T-tests are the last line of statistical analysis for investigating potential correlations between two sets of means. The testing involves randomly chosen samples from the two classes or groups. It is a type of statistics that uses non-perfectly normal distributions and random sample selection. Whether the models being studied are from the same or other categories determines which T-test will be performed. The conclusion drawn from this process shows how likely the differences in the means occurred purely by chance. The test is beneficial for comparing population age, duration of crops from two distinct species, student grades, etc.
Comprehending the t-test concept
A T-test compares data from two sample populations to determine whether one would provide a significantly different result. Distribution patterns and sample variation both have a role in determining how well this test performs. The test is run, and a T-value is calculated as the statistical inference of the likelihood that the typical outcome is driven by chance, given the given parameters.
For instance, a T-test may be used to compare the average petal length of various species' flowers to determine whether they belong to the same genus. The user can get a conventional conclusion by randomly selecting petals from two different flower species. There are two possible routes to the ultimate T-test interpretation:
· If the difference between the means is 0, then the null hypothesis states that the means must be equal.
· The alternative hypothesis holds if the difference between the means equals zero. This hypothesis contradicts the null hypothesis, suggesting that the observed phenomena are not coincidental.
However, this T-test is legitimate and should be performed when comparing the mean or average of two categories or groups. It is not advised to do so whenever there are more than two comparisons to be done.
The t-test is among numerous tests that provide this function. For more extensive samples and more variables, statisticians have access to different tests beyond the t-test. Statisticians employ a z-test for extensive samples. The chi-square test and the f-test are two more common statistical methods.
Assumptions of the T-test
The following are the presumptions upon which the test is conducted:
i. Data displayed against the T-test distribution should look like a bell curve if it follows a normal distribution.
ii. A larger sample size will produce a more distinguishable bell curve.
iii. The standard deviations of the samples should be about equivalent; hence the variance should be set such that this is the case.
iv. These hypotheses are tested using a continuous or ordinal scale of measurement. Parameters and variations affecting samples and contexts are considered based on conventional wisdom.
v. Random sampling is used in all of the experiments. The validity is frequently questioned because of the lack of control over the samples.
T-Test algorithm
The t-test needs three pieces of mandatory information. The mean difference (the difference in means across groups), the standard deviation (the variation in means between groups), and the number of data values (the range of individual values) are all examples.
By comparing the two, we can see whether the difference is statistically significant or falls within the margin of error. The outcome of the t-test consists of two numbers: the t-value and the number of degrees of freedom. The t-value, also known as the t-score, is a metric for comparing two samples by dividing the difference in means by the range of values found within the samples.
The numerator represents the dissimilarity in means between the two collections of data. The denominator quantifies the dispersion or variability within the sample sets.
The T-distribution table is a critical value table against which this calculated t-value is compared. A high t-score indicates a wide disparity between the two samples. The smaller the t-value, the higher the similarity between the two samples. The t-score, also known as the t-value, is a statistical metric of the degree to which two groups are dissimilar. The relevance and robustness of the null hypothesis can only be evaluated by considering the research values subject to variation.
Categories of T-test
The following are examples of popular forms of T-tests:
i. One-sample T-Test
The average of one group is contrasted to the estimated value or means of the population when completing this test. One-sample t-tests use the following formula as their basis:
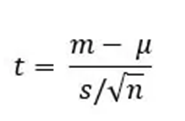
Where:
· t = t-statistic
· m = mean of the group
· µ = theoretical mean value of the population
· s = standard deviation of the group
· n = sample size
ii. Independent two-sample T-test
Samples from two distinct populations, species, or groupings are compared using this method. It is sometimes called a T-test for independence. It is determined using the following T-test formula:
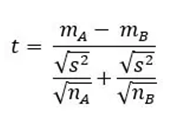
Where:
· mA – mB = means of samples from two different groups or populations
· nA – nB = respective sample sizes
· s2 = standard deviation or common variance of two samples
iii. Paired sample T-test
When the two samples come from the same population or category, we may test the null hypothesis that they are not different. The groups are examined twice, once at each time point or under each experimental condition. The t-value may be calculated using the following formula:
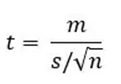
Where:
· t = t-statistic
· m = mean of the group
· s = standard deviation of the group
· n = sample size
iv. Equal variance T-test
When the variance of the two data sets is comparable or when there is an equal number of people in each group or population, this test may be performed. The pooled T-test is another name for this analysis. The formula is as shown below:
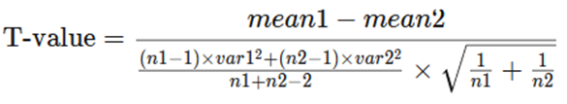
Where:
· Mean1 and mean2 = average value of each set of samples
· var1 and var2 = variance of each set of samples
· n1 and n2 = number of records in each set
and,
Degrees of freedom = n1 + n2 − 2
Where:
· n1 and n2 = number of records in each sample set
v. Unequal variance T-test
The unequal variance testing method is used when there is a discrepancy between the sample sizes and the variances. The formula for what is often known as "Welch's test" is:
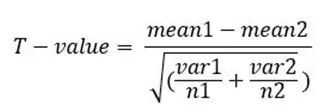
Where:
· mean1 and mean2 = Average value of each set of samples
· var1 and var2 = variance of each set of samples
· n1 and n2 = number of records in each set
and;

Where:
· var1 and var2 = variance of each of the sample sets
· n1 and n2 = number of records in each sample set
Application of the T-test
Only when contrasting the means of two given categories (also known as a pairwise comparison), can a t-test be employed. Use an ANOVA or post hoc test if you have to contrast multiple types or if you need to make numerous pairwise comparisons.
In contrast to non-parametric testing, parametric tests like the t-test assume that your data is usually distributed. The t-test presupposes that the data you have:
· are uncorrelated;
· are normally distributed;
· and exhibit homogeneity of variance (i.e., the same amount of variation across all groups).
Non-parametric alternatives to the t-test, like the Wilcoxon Signed-Rank test, are available if your data do not satisfy these assumptions.
Test statistics (T-values) and probability (P-values)
The p-value from a t-test indicates how likely your results result from random chance alone. P-values range from 0% to 100% and are typically expressed as a decimal (for instance, a p-value of 5% is 0.05). If your p-value is low, your data is probably not a fluke. For example, a p-value of .01 suggests there is only a 1% likelihood that the outcomes from an experiment occurred by coincidence.
T-distribution
The t-distribution, sometimes called the Student's t-distribution, has a bell-shaped distribution with heavier tails than the normal distribution. It is used when a large enough sample size is unavailable, or the variation of the population being studied is unclear. T-distributions have broader tails than normal distributions because of the increased likelihood of outlying values. In statistics, t-tests are calculated using the t-distribution.
What is the function of the T-distribution table?
One-tail and two-tail versions of the T-Distribution Table are also available. The former is used when a single, unambiguous value or range of values may be assigned a positive or negative evaluation. How likely is it, for instance, that the result will be more than seven on a die roll or that the output number will stay less than -3? The latter is used in the range-bound analysis, asking questions like "Do these coordinates lie between -2 and +2?".
Contrasting the t-test with the Chi-square test
The t-test is a parametric evaluation that lets us compare two sets of statistical data to see whether there is a significant difference. Conversely, using a non-parametric approach, the chi-square test determines whether or not two samples or variables are correlated.
Common errors in the t-test algorithm
· The use of an incorrect equation is a common error. The kind of data is most useful for analysis, and the research issue determines which tests are appropriate. If you use the wrong formula, your calculations might be off.
· Sample standard deviation incorrectly calculated. The t-test formula requires the sample standard deviation. Inaccurate findings may occur from using the incorrect formula or from calculation errors.
· An error can come about due to not verifying the assumptions. The equality of data and variances between the two groups is assumed in this test. We risk getting inaccurate findings if we break these assumptions.
· Sample sizes and assumptions about the variances of the two groups being compared determine the number of degrees of freedom in the t-test calculation. Results may be off if the wrong number of degrees of freedom is used.
· Incorrectly interpreting the results: We must accurately interpret the findings even if the test is carried out correctly. Knowing how the p-value and confidence interval apply to the study's central issue is also essential.
Challenges of the T-test technique
i. It is susceptible to outliers or extreme numbers that have an atypical effect on the overall picture. It does, however, occur often in the actual world.
ii. It has the same potential for Type I error as any statistical test: the chance of falsely rejecting the null hypothesis.
iii. Data within each group is assumed to have a normal distribution (i.e., the normality assumption). However, in practice, particularly with little data, normalcy cannot always be assumed.
iv. Reliability decreases with decreasing sample size. It is a drawback since getting big sample sizes might sometimes be difficult.
v. It presumes the independence of observations within each set. However, getting objective data in the real world may be impossible.
Uses of the t-test in the real world
i. The paired sample test is helpful in medical research since it allows us to compare patients' performance before and after treatment.
ii. The independent two-sample test may examine demographic data such as age, weight, and sexual orientation in population samples.
iii. Commercially, this metric helps gauge the success of advertising initiatives.
iv. It may also calculate whether or not routing deliveries from the vendor to the customer would save time.
v. It may provide light on how adjustments to the production process affect key performance indicators.
Conclusion
The t-test is a statistical inference that compares the means of two groups and establishes if there is a substantial difference between them. Like the data set obtained by flipping a coin 100 times, T-tests are employed when the data sets reflect a normal distribution and contain unknown variances. In statistics, the t-test is used to test hypotheses; it calculates statistical significance based on the t-statistic, the values of the t-distribution, and the degrees of freedom.
