What does poisson distribution imply?
A Poisson distribution is a theoretical function distribution used in statistics to illustrate the number of times an event is predicted to occur over a certain period. It is, in essence, a count distribution. Poisson distributions are frequently used to analyze independent events that occur consistently during a specified time frame. It was named after Siméon Denis Poisson, a French mathematician.
The poisson distribution is a discrete function, implying that the variable may only take values from a (possibly endless) list. To put it another way, the variable cannot accept all values in any continuous range. The variable in the Poisson distribution may only take whole integer values (0, 1, 2, 3, etc.), not fractions or decimals.
The background of the poisson distribution
The poisson distribution, like most statistical tools and probability measurements, was developed in the gaming industry. Siméon Denis Poisson, a French mathematician, devised the distribution in 1830 to represent the low to the high spread of the expected number of times a gambler would most likely win at a gambling activity, for instance, baccarat, within a large number of times the game was played. Unfortunately, the gambler ignored Poisson's forecast that he would only win a fixed number of times and lose substantially.
Poisson's statistical tool's wide variety of prospective uses became clear some years later, during World War II when a British statistician deployed it to examine bomb strikes in London. R.D. Clarke improved the Poisson Distribution as a statistical framework. He sought to persuade the British government that the German bombs fell at random or entirely by chance and that its adversaries had adequate intelligence to target specific city regions. The Poisson Distribution has since been used in various disciplines of study, including medicine, astronomy, commerce, and sports.
The validity of the poisson distribution
Under certain situations, the Poisson Distribution is a valid probability assessment tool. In case all of the following necessities are met, the statistical model is right:
· k being the number of times an event occurs during a certain period, and its potential values are simple numbers such as 0, 1, 2, 3, 4, 5, and so on.
· The occurrence of the event under consideration does not affect the likelihood of the event reoccurring (events occur independently).
· The event in issue cannot happen twice at the same moment. There needs to be some gap of time separating repetitions of the event, even if it is only half a second.
· The likelihood of an event occurring within a smaller fraction of the whole-time frame under consideration is related to the duration of that smaller period section.
· The total number of trials, and chances for the event to occur, is significantly bigger than the number of times the event occurs (which means that the Poisson Distribution is only intended to be utilized for relatively infrequent events).
Given the abovementioned requirements, k is a random variable with a Poisson distribution.
The formula of poisson distribution
The Poisson Distribution formula is shown below, where μ denotes the mean (average) number of occurrences during a certain time frame. The probability formula is as follows:
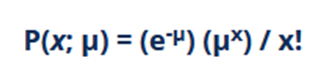
Where:
x = the number of times an event occurs in a certain period
e, Euler's number = natural logarithm base is around 2.72.
x! = the inverse of x
λ = expected value (EV) of x when that is also equal to its variance
Characteristics of a poisson distribution
· The experiment involves counting the events that will occur within a certain period or in a specific distance, area, or volume.
· An event's odds are the same for any time, distance, area, or volume.
· Each occurrence is distinct from the others. For example, the number of individuals arriving in the first hour is independent of those arriving in any subsequent hour.
Business applications of the poisson distribution
The Poisson Distribution may be realistically applied to various typical commercial procedures across businesses. As previously stated, using the Poisson Distribution to analyze operations may give the firm management valuable perspectives on operational efficiency levels and recommend solutions to raise productivity and enhance operations.
Here are some examples of how a corporation may use Poisson Distribution analysis:
· Examine the variations in commercial insurance coverage.
Assess the annual average number of losses or claims covered by the organization's commercial insurance. Then, using a Poisson probability computation, establish the maximum and least number of claims that might be made in any given year.
Examine the cost of your insurance as well as the coverage it offers. Consider if you are overpaying - meaning that you are paying for a coverage level that, given the likely maximum number of claims, you probably do not need.
On the contrary, you may discover that you are underinsured, which means that if the Poisson distribution predicts the greatest number of claims in a given year, your insurance coverage would be insufficient to pay the losses.
· Assess whether there is sufficient customer service personnel.
Determine the average number of client service calls handled per hour that take more than 10 minutes. Then, use the Poisson Distribution to determine the most likely maximum number of calls per hour that will require more than 10 minutes. Suppose that the maximum number of 10-minute calls happens; consider whether the client service workforce is sufficient to handle all calls without putting consumers on hold.
· Use the Poisson formula to determine whether keeping an outlet open 24 hours daily is economically viable. Compute the outlet's average sales for the nighttime shift, which runs from midnight to 8 a.m. Calculate the likely lowest number of sales that might be produced during the nighttime shift using the distribution formula.
Finally, consider if the lowest likely sales number reflects enough money to pay all the expenditures (wages and salaries, power, etc.) of keeping the shop open during that period while still delivering a healthy profit.
Application of poisson distribution in statistical analyses
This probability distribution is commonly used by analysts in survival analysis, insurance analysis, and quality control
· You may use the Poisson distribution to calculate the probability for counts of occurrences.
· The Poisson distribution is used in hypothesis testing to determine the rate of occurrence. Poisson Rate Tests, for instance, can assess whether the difference in the number of customer complaints each day at two locations is statistically important.
· Variations in the independent variables correlate to shifts in the counts of events measured by the dependent variable, according to Poisson regression models.
Poisson distribution requirements
When the following requirements are met, a variable follows a Poisson distribution:
· Data are event counts.
· Each occurrence is independent.
· During the study period, the average rate of incidence did not vary.
The last two principles are related to a statistical assumption known as Independent and Identically Distributed (IID) Data.
Finance and the poisson distribution
The Poisson distribution is also frequently used to describe financial count information where the total is modest and often zero. In finance, for example, it may be used to estimate the number of deals a particular trader can make in a given day, which can be 0 (frequently), 1, or 2, and so on. As a further instance, this framework may be used to forecast the number of market "shocks" that will occur during a specific time, such as a decade.
Comparison between the poisson and binomial distributions
Since they both represent the occurrence of events, the Poisson and binomial distributions are subject to comparison. The Poisson distribution, on the other hand, has no upper limit on the number of observations per unit.
Contrary to this, the binomial distribution computes the likelihood of an event happening a certain number of times in a certain number of trials. It assesses the probability of X occurrences occurring within N trials. The number of occurrences (X) cannot exceed the number of trials in the binomial distribution.
When should you use the poisson distribution?
The Poisson distribution best suits statistical analysis when dealing with a count variable. For example, X is frequently based on one or more explanatory factors. For example, to predict how many faulty goods would be produced on a manufacturing line given certain inputs.
Cumulative poisson probability
A cumulative Poisson probability is the likelihood that the Poisson random variable (X) will fall inside a particular range. Consider the chance of obtaining AT LEAST n successes in a Poisson experiment. In this case, n is a Poisson random variable. In addition, the cumulative Poisson probability is the probability that n falls between 0 and n.
For example, we may be curious about how many phone calls a receptionist receives in an hour. Assume we knew she received one phone call every hour on average. What are the chances she will receive AT LEAST ONE phone call in the next hour? A cumulative Poisson probability would be the likelihood of receiving AT LEAST ONE phone call in the following hour.
In this case, the cumulative Poisson probability equals the probability of receiving zero phone calls and the likelihood of receiving one. As a result, the cumulative Poisson probability would be 0.368 + 0.368 = 0.736.
The cumulative Poisson probability notation is best described by example. P(X 1) denotes the probability of receiving LESS THAN 1 phone call; P(X 1) represents the chance of receiving AT MOST 1 phone call; P(X > 1) denotes the probability of receiving AT LEAST 1 phone call, and P(X > 1) denotes the probability of receiving MORE THAN 1 phone call.
What are the poisson distribution's assumptions?
To be correct, all events must be independent, the pace of occurrences must be steady across time, and events cannot occur concurrently. Furthermore, the mean and the variance will be equal.
What is the distinction between the poisson distribution and the poisson process?
The poisson process is the progressive occurrence of separate events, such as a human's steady heartbeats. The poisson distribution determines the likelihood of an event repeating numerous times in a certain period, for instance, how many times an event in the poisson process happens. A probability distribution, for example, is the likelihood of having a certain number of heartbeats in one minute.
What is the distinction between a normal distribution and a poisson distribution?
The main distinction between the Poisson and normal distributions is that the Poisson is discrete while the normal is continuous. When the Poisson distribution's mean increases, it resembles the normal distribution.
Conclusion
The Poisson Distribution is a method used in probability statistics to forecast the variation from a known average rate of occurrence within a specific period. Hence, if the average rate at which a particular event occurs during a given time frame is known or can be computed, the Poisson Distribution can be employed as follows:
· To predict the most likely maximum and lowest number of times the event will occur during the time limit indicated
· To estimate how much deviation there will be from the average number of occurrences
Corporations can use the Poisson Distribution to investigate how they might be able to enhance their business effectiveness. For example, a Poisson Distribution study can highlight how a corporation might better arrange employees to manage peak hours for customer support calls.
