What Is the Durbin-Watson Test?
The Durbin-Watson test, developed by economists James Durbin and Geoffrey Watson in the early 1950s, is a statistical test used to detect the presence of autocorrelation in the residuals of a regression model. It specifically focuses on detecting first-order autocorrelation, where the correlation exists between adjacent observations. The test is applicable to both time series data, where observations are collected over time, and cross-sectional data, where observations are collected from different individuals or entities at a specific point in time.
The Durbin-Watson test statistic is denoted by the symbol "d." Its value ranges between 0 and 4, with 2 being the critical value around which inference is made. The test statistic measures the degree of autocorrelation present in the residuals of a regression model. A value of d equal to 2 implies no autocorrelation, while values below 2 indicate positive autocorrelation, and values above 2 indicate negative autocorrelation.
How Does the Durbin-Watson Test Work?
To perform the Durbin-Watson test, we start by estimating a regression model using the method of least squares. Next, we obtain the residuals, which represent the differences between the observed and predicted values of the dependent variable. These residuals are then used to calculate the Durbin-Watson test statistic.
The test statistic is computed as follows:
What Is the Durbin-Watson Test?
The Durbin-Watson test, developed by economists James Durbin and Geoffrey Watson in the early 1950s, is a statistical test used to detect the presence of autocorrelation in the residuals of a regression model. It specifically focuses on detecting first-order autocorrelation, where the correlation exists between adjacent observations. The test is applicable to both time series data, where observations are collected over time, and cross-sectional data, where observations are collected from different individuals or entities at a specific point in time.
The Durbin-Watson test statistic is denoted by the symbol "d." Its value ranges between 0 and 4, with 2 being the critical value around which inference is made. The test statistic measures the degree of autocorrelation present in the residuals of a regression model. A value of d equal to 2 implies no autocorrelation, while values below 2 indicate positive autocorrelation, and values above 2 indicate negative autocorrelation.
How Does the Durbin-Watson Test Work?
To perform the Durbin-Watson test, we start by estimating a regression model using the method of least squares. Next, we obtain the residuals, which represent the differences between the observed and predicted values of the dependent variable. These residuals are then used to calculate the Durbin-Watson test statistic.
The test statistic is computed as follows:
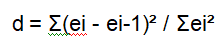
Here, ei represents the residuals, and ei-1 represents the lagged residuals. The summation is performed over all the residuals.
Interpreting the Durbin-Watson Test Statistic
The Durbin-Watson test statistic provides valuable insights into the presence and nature of autocorrelation in a regression model. The following interpretations are commonly applied:
d = 2: This indicates no autocorrelation. The residuals are independent, and the regression model is appropriate for further analysis.
d < 2: A test statistic below 2 signifies positive autocorrelation. This implies that adjacent residuals have a tendency to be positively correlated, indicating that the model underestimates the true level of correlation. In this case, the coefficient estimates may be inefficient, and standard errors could be biased, leading to unreliable inference.
d > 2: A test statistic above 2 suggests negative autocorrelation. Here, adjacent residuals tend to have a negative correlation, indicating that the model overestimates the true level of correlation. Similar to positive autocorrelation, this situation can result in biased coefficient estimates and unreliable inference.
Significance of the Durbin-Watson Test
The Durbin-Watson test plays a vital role in statistical analysis by allowing researchers to identify and account for autocorrelation. By examining the residuals of a regression model, the test helps in assessing the validity of the model and drawing accurate conclusions. Moreover, it aids in the selection of appropriate diagnostic techniques and remedial actions to handle autocorrelation-related issues.
Remedies for Autocorrelation
If the Durbin-Watson test suggests the presence of autocorrelation, several strategies can be employed to address the issue:
Include additional relevant variables: Autocorrelation may arise due to omitted variables. Adding these variables to the model can help capture the unaccounted correlation and mitigate the problem.
Transform the data: Sometimes, transforming the dependent or independent variables can reduce or eliminate autocorrelation. Common transformations include differencing or taking logarithms.
Use a different model specification: Alternative regression techniques, such as time-series models like ARIMA (AutoRegressive Integrated Moving Average), may be better suited to handle autocorrelated data.
Apply autoregressive techniques: Autoregressive models explicitly account for autocorrelation and can provide more accurate predictions and reliable parameter estimates.
Example of the Durbin Watson Statistic
To better understand the Durbin-Watson statistic, let's consider a hypothetical example involving a regression model. Suppose we are examining the relationship between the number of hours studied (independent variable) and exam scores (dependent variable) for a group of students.
We collect data from 30 students and run a simple linear regression analysis. After estimating the model and obtaining the residuals, we want to assess if there is any autocorrelation present in the residuals using the Durbin-Watson test.
Here is a table presenting the observed exam scores and the corresponding residuals:
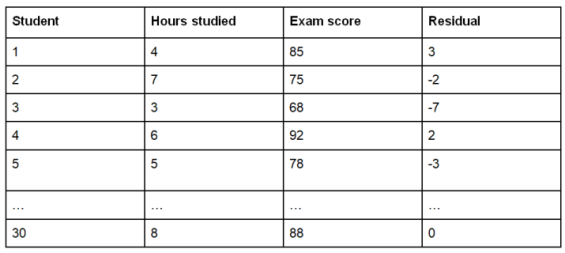
To calculate the Durbin-Watson statistic, we need to compute the squared differences between adjacent residuals:
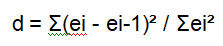
Let's perform the calculations:
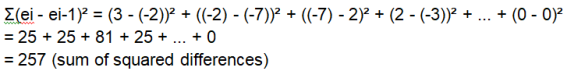
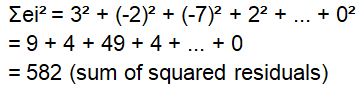
Now, we can substitute these values into the formula:
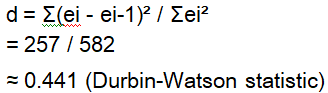
Interpreting the Durbin-Watson statistic:
In our example, we obtained a Durbin-Watson statistic of approximately 0.441. Since this value is less than 2, it indicates the presence of positive autocorrelation in the residuals. This suggests that there is some degree of correlation between the residuals of adjacent observations. Therefore, our regression model may not fully capture the underlying autocorrelation, and the coefficient estimates and inference results may be biased or unreliable.
Upon detecting autocorrelation, further diagnostic analysis and remedial actions should be considered to address this issue, as mentioned in the previous article section.
Note: The example provided is for illustrative purposes only and does not reflect actual data. The calculations and interpretation are simplified for clarity.
Conclusion
The Durbin-Watson test is a powerful statistical tool used to detect autocorrelation in regression models. By examining the residuals, it enables researchers to identify the presence of autocorrelation and make informed decisions about appropriate model specifications and remedial actions. Understanding and addressing autocorrelation is crucial for ensuring the validity and reliability of statistical analysis. The Durbin-Watson test, along with other diagnostic tools, empowers researchers to account for autocorrelation and derive meaningful insights from their data.
